Location: Home >> Detail
TOTAL VIEWS
Crop Breed Genet Genom. 2019;1:e190019. https://doi.org/10.20900/cbgg20190019
Département de phytologie, Pavillon Charles-Eugène Marchand 1030, Ave., de la Médecine, Quebec City, QC, G1V 0A6, Canada
* Correspondence: François Belzile.
This article belongs to the Virtual Special Issue "Genetic Gains in Plant Breeding"
Introducing genomic prediction approaches at an early stage (i.e., selecting the best crosses) is less disruptive than at advanced stages (identifying the best progeny) in terms of the breeding process and resources involved. Here, we tried to assess the reliability of a predictive approach in an applied breeding context. First, we developed a genomic selection model to estimate trait values and validated it on existing progenies. It was then used to predict the mean (µ) and genetic variance (VG) for each cross among a large set of simulated progenies. The degree of agreement between predicted and observed values for key traits indicated that the predictive model provided an adequate degree of accuracy. Crosses predicted to be superior produced progeny that persisted longer in the breeding process suggesting that the predictions are consistent with reality. The predicted correlations between traits known to be correlated (e.g., DON-GYD) were concordant with observed and expected correlations signifying that the properties of these simulated progeny were in line with expectations. Among the 30,000 potential crosses that could be made between lines comprising the training population, only 2.2% were predicted to exhibit a low correlation between DON and GYD and just 0.13% were predicted to produce progeny in which the top lines could combine high GYD with reduced DON. Even in the absence of empirical proof that genomic prediction can outperform classical practice, the results obtained here appear encouraging regarding the potential of such an approach in barley breeding programs.
Genomic prediction aims to increase the rate of genetic gain for complex quantitative traits [1,2]. Depending on the purpose of the prediction, it can be divided into two approaches: genomic selection (GS) and genomic mating (GM). In GS, phenotyped and genotyped lines are used to predict the performance of non-phenotyped progeny based solely on genotypes [3]. In GM, phenotyped and genotyped individuals are used to predict the performance of progeny from simulated crosses [4].
The ability to predict complex quantitative traits solely from genotypic data (molecular markers) is a desirable goal for plant breeding programs [5]. During the last decade, much work has been done to optimize GS models in plants, but practical implementation of GS in breeding programs remains limited [6–10] as the shift from phenotypic to genomic selection entails major changes in resource allocation and logistics [11]. In GS, genome-wide genotypic data are used to estimate trait values for each line derived from crossing a pair of parental lines and to select the most promising lines. Endelman [12] was the first to propose another application of these statistical models where these molecular markers can be used in a GM approach to design the crossing schemes in a breeding program, by estimating the value of each pair of parental lines (as reflected in the predicted performance of their simulated progeny) and selecting the best pairs to initiate the development of new varieties [13].
The ability to predict the potential of a cross, before it is created, would allow a more efficient use of the genetic and financial resources of a breeding program [14]. In many selfing crops, pure-breeding varieties are developed from populations resulting from crosses made between two parents. Testing large numbers of parents leads to an excessively high number of biparental populations to test [15]. Even though breeders try to take into account all potential information about parents to design crosses, many crosses are eliminated each year because they do not produce superior progeny [16,17]. In a broad statistical sense, the potential value of a cross is a function of the mean and variance of a population [18,19]. The identification of the most promising crosses therefore rests on adequately predicting the mean and variance for high priority traits within large sets of potential crosses [2].
The classical theory of quantitative genetics predicts the mean of a population of progeny as the mean performance of both parents [4,12,13]. Thus, for each cross, the mean can be calculated as the mean of the parents’ GEBVs, based on the estimation of single-nucleotide polymorphism (SNP) effects obtained with a statistical model [2,14,17,20]. Unlike the mean, the prediction of genetic variance is based on the knowledge of population parameters (often unknown)[4,20], which makes it inherently more difficult to predict [2,19,21–24]. Initial studies tried to tie genetic variance to factors such as coancestry [21,25,26], phenotypic distance [23], genetic distance [27] or a combination of the above [21–23,28,29]. These methods quickly showed a low predictive ability for genetic variance [4,20,24,30].
This predictive weakness has been proposed to be mainly due to the fact that the segregation of loci is not taken into account [2,24,30,31], especially for the methods based on phenotypic distance. Moreover, the methods based on coancestry and genetic distance measure coancestry/distance across the entire genome, including a majority of mostly neutral loci, and do not provide predictions for each trait [2].
As molecular markers became more accessible, researchers have extended these methods to genome-wide markers (such as SNPs). Initially, Endelman [12] estimated genetic variance from the effects of SNPs, taking into account linkage equilibrium between markers. Recently, methods based on explicit modeling of the segregation of loci have been proposed and seem to have greater predictive ability for genetic variance [17,30]. The ability to estimate the effects of SNPs, coupled with accessible and powerful computing resources, has led to new approaches for predicting genetic variance based on the simulation of biparental populations derived from large numbers of potential crosses [13,20].
The genetic gain achieved within a population depends on the phenotypic variance of the candidates for selection. Therefore, crosses with large genetic variance (and hence phenotypic variance), would theoretically contribute to increased genetic gain [20]. A successful cross should generate a population with a favorable mean and a large genetic variance [2,4]. Within such progeny we can hopefully identify lines superior to both parents, a phenomenon known as transgressive segregation [20].
In barley, initial studies suggest that some traits can be improved by selecting crosses with a favorable mean and variance [2,32]. Although these results are encouraging, additional validation work is needed to support their application in breeding programs. In this study, we tried to assess the reliability of a predictive model in an applied breeding context. First, we developed a genomic selection (GS) model to predict trait values for existing progeny already developed and evaluated within a breeding program. This genomic selection model was then used to examine the realm of possibilities among a large set of potential crosses. One of the focal points of this work was to identify crosses in which the undesirable correlation between high grain yield and low DON content was predicted to be weakened.
We used two populations: a training population (TP) and a set of selection candidate (SC) lines. The TP was composed of 245 advanced lines, varieties and some sources for fusarium head blight (FHB) resistance chosen to represent the genetic diversity of a six-row barley breeding program (at Université Laval, UL, Canada) in Eastern Canada. This population was used to train prediction models for GS and GM. The set of SCs comprised 350 F5 lines derived from eight crosses between a total of eight parents that were part of the TP. As a means to assess the accuracy of our trained genomic selection model (described below), we predicted phenotypes for SC lines and the most promising 10% (35 lines), mostly based on yield, were selected and evaluated in the field as described below.
For the TP, we recovered historical phenotypic data from official registration trials performed in 14 locations in the provinces of Quebec and Ontario from 2004 to 2015. This provided data for 14 to 41 environments (location × year) depending on the trait (Supplementary Data 1). Five key traits were investigated in this study (1) deoxynivalenol content in kernels (DON), (2) heading time (HTM), (3) days to maturity (MAT), (4) thousand kernel weight (TKW) and (5) grain yield (GYD). DON was evaluated in artificially-inoculated FHB nurseries in two-row plots 0.65 to 1 m in length, spaced 17 cm apart and at a planting density of 375 plants m−2. The experimental design was a randomized complete block with two replications. Field trials for agronomic traits (HTM, MAT, TKW and GYD) were conducted in four-row plots (4 to 5 m in length, 17-cm row spacing and a planting density of 375 plants m−2) in a randomized complete block design with two replications. For SC lines, phenotypic evaluations similar to those conducted for the TP (same traits and experimental design) were performed in two to four environments depending on the trait. The methodology used for the measurement of each trait is detailed in Supplementary Data 1.
Phenotypic Data and AnalysisAn analysis of variance (ANOVA) and an estimation of broad-sense heritability He2 were performed for each environment using the META-R program v. 6.04 [33]. Broad-sense heritability was computed as He2 = σG2/(σG2 + σe2/r), where σG2 is the genetic variance, σe2 is the error (residuals) variance, and r is the number of replicates. Environments displaying a very low He2 (<0.40) and no significant difference among lines were filtered out. As all lines were not evaluated in all environments, best linear unbiased estimations (BLUEs) across environments were computed using META-R. Following the model:
we estimated a BLUE for each line, where yijk is the observed phenotype, μ is the overall mean, Envi is the random effect of the ith environment (a location-year combination), Repj(Envi) is the random effect of jth block nested within the ith environment, Linek is the fixed effect of the kth line, EnviLinek is the random effect of the interaction between the ith environment and kth line and eijk is the random error term. A single phenotypic value for each trait and each line across all environments was provided by the BLUE and this was used to train the prediction models.
Phenotypic data for the SC lines were similarly estimated as a BLUE using META-R. The variance components and the broad-sense heritability He2 in each environment were computed as specified above. Similarly, a single phenotypic value for each trait and each line across all environments was provided by the BLUE and this was used to validate the predictions as described below. The phenotyping of TKW was performed on a composite of two replicates. Hence, the phenotypic value was simply the mean across environments and the variance components were generated by considering environment as replicate.
Genotypic Data GenotypingUsing a CTAB-based protocol, genomic DNA was extracted from 5 mg of dried young leaves. Using a fluorometric quantification method (PicoGreen, Eugene, USA), the DNA concentration (ng/µL) in each sample was then measured. A total of 200 ng per sample was used for the preparation of PstI/MspI GBS libraries in a 96-plex design [34] and the optimized protocol is detailed in Abed et al. [35]. After amplification and purification, each of the GBS libraries was sequenced on two Ion PI chips (Thermo Fisher Scientific, Waltham, Massachusetts, USA) for the TP and one Ion PI chip for the SCs on an Ion Torrent Proton sequencer at the Plateforme d’analyses génomiques (IBIS, Université Laval).
SNP calling and filtration procedureUsing the Fast-GBS pipeline [36] and based on the IBSC reference genome (Ensembl Plant, Barley genome IBSC_v.2)[37], informative SNPs were identified. Single-nucleotide polymorphisms were identified using reads ≥50 nucleotides in length and if supported by ≥2 reads. Moreover, SNP loci having more than 10% heterozygous genotypes and >80% missing data were filtered out. Finally, using Beagle v. 4.1 [38], residual missing data were imputed and only SNPs with a minor allele frequency (MAF) ≥5% for the TP and ≥15% for the SCs were kept.
For the GS phase aiming to predict trait values for SC lines, we identified SNPs common to the TP and SCs using VCFtools [39] and extracted them from the SC SNP catalogue. Using the Merge function in TASSEL v. 5.2.31 [40], we concatenated the common SNPs present in the collection of SCs with the entire SNP set in the TP to constitute a single unified SNP catalogue. The missing genotypes in the SCs were imputed from the TP information using Beagle v. 4.1 [41].
Assignment of SNP genetic positionsFor the GM work aiming to predict trait values among simulated progeny of potential crosses, it was necessary to provide a genetic map position for each SNP marker. This information was needed to infer recombination events and generate simulated progeny populations (RILs) for pairwise crosses between all lines present in the TP. To assign a genetic position to each SNP, we first extracted FASTA sequences corresponding to 100 pb surrounding each SNP using an R script [42]. Furthermore, using Barleymap [43], we mapped them on the POPSEQ genetic map [44] in order to have their genetic position.
Genomic Prediction Approaches Genomic selectionStatistical model
The statistical model used in this study was fitted using the Bayesian framework. Based on results obtained in previous work [45], we used a model with linear kernel (GBLUPe) capturing both additive and non-additive epistatic effects with a variance–covariance matrix. The GBLUPe is a linear mixed model that can be written as follows:
where y is the vector of phenotypic records (response variable), μ is the general mean and considered as a fixed parameter, u1, ε are random parameters with ε~MN(0, σε2I) is the error term and u1~MN(0, σu12K) is a vector of random additive effects with K = G; a genomic relationship matrix among lines, computed following the method described by Cuevas et al. [46]. In the term u2~MN(0, σu22H), H = G#G , and # stands for the Haddamart product or cell-by-cell product, this random term allows the model to capture epistatic effects [47]. Because of K = G, this model is considered equivalent to genomic BLUP (GBLUP)[48] with epistatic effect. We implemented GBLUPe in the R package BGLR [49] using 100,000 iterations of Gibbs sampling, a burn-in of 10,000 and a thin of 10.
Validation of genomic selection
We first assessed the accuracy of the GS model by performing 60:40 cross-validations (60% of lines used to train the model and 40% used to validate the model). Such cross-validation was repeated 100 times (by randomly selecting lines to assign to each subpopulation). The accuracy was measured as Pearson’s correlation between the predicted and the observed performance (BLUEs) for the lines assigned to the validation subpopulation. The mean and standard errors across the 100 iterations were computed for each trait.
For a further assessment of GS accuracy, we performed a validation with an external population. All lines present in the TP were used to fit the GBLUPe models and to predict the performance (for DON, HTM, MAT, TKW and GYD) of 350 SC lines. A selection intensity of 10% was used such that 35 SC lines were selected on the basis of the best overall predicted performance. These selected lines were then phenotyped in two to four environments. The prediction accuracy was measured as Pearson’s correlation between the predicted and the observed performances across all environment (BLUEs). As a final comparison, a coefficient of correlation was computed between the observed and predicted phenotypes based on the ranking of the SC lines (Spearman’s coefficient of correlation).
Genomic matingUsing the procedure implemented in the PopVar R package [20], we predicted the trait values for simulated progeny of all pairwise crosses between all lines of the TP. Recombination between marker loci was simulated on the basis of the genetic map positions of the SNPs forming the TP dataset. Simulated populations of RILs of all possible crosses between lines in TP were then generated. The simulation process was iterated 50 times in order to reduce the effects of sampling error; each iteration was based on 500 progeny per cross. Using the trained model (see above), we estimated the effect of each SNP in order to compute the GEBV of each simulated RIL. For each RIL population (derived from a cross), and based on GEBV, the population mean (μ), the genetic variance (VG) and the mean of superior progeny (top 10%; μsp) for each trait were computed.
Validation of genomic mating
In order to evaluate the accuracy of the predicted value of a cross, we performed a retrospective validation. Through this procedure, we assumed that superior crosses would be expected to produce progeny that persist longer in the breeding program. To achieve this, we recovered information about the persistence over generations of progeny from 210 crosses carried out from 2004 to 2010 and evaluated at UL and in a private breeding program (Céréla Inc, Saint-Hugues, Québec, Canada) located in the same broad geographic area. All these crosses involved parents present in the TP for which we had predicted μ and VG for the five traits using PopVar.
Depending on the trait that had been emphasized during the selection process, we investigated two different situations. In the first situation, crosses were designed in a conventional cultivar development process where emphasis was focused mostly on GYD; we assessed the persistence of 70 and 50 crosses made and evaluated within the UL and Céréla breeding programs, respectively. In the second situation, crosses were selected more in the context of pre-breeding (aiming to develop improved germplasm and not cultivars per se) and in which emphasis was placed first on DON. A set of 90 crosses were developed and selection was first performed based on DON concentrations in nurseries. We then assessed the persistence of these 90 crosses in the selection process.
Selecting the best crosses
First, we assessed the presence of promising crosses (with a more favorable correlation between GYD and DON) by computing, for all possible pairwise crosses in the TP, the Pearson correlation (r) between GEBVs for GYD and DON within each population. We defined promising crosses as those exhibiting an rGYD-DON ≤ 0 meaning that high yield is no longer associated with high DON. As a validation of such predictions, we measured the correlations between predicted trait values for pairs of traits known to be strongly correlated (HTM-MAT and GYD-TKW). Furthermore, focusing on important traits (GYD and DON), we computed correlated responses (Cr) which is the mean of the μsp for GYD and the corresponding mean for DON for the set of promising crosses (rGYD-DON ≤ 0) previously identified in order to detect crosses predicted to offer a high mean yield. Crosses were considered to offer superior yield when the mean of μsp for GYD and mean of corresponding lines for DON was equal or better than that of checks used in registration trials in Eastern Canada. Based on the best statistical model (GBLUPe) we predicted trait values (GEBVs) for four to six checks used in GYD and DON trials, respectively.
Genotypic characterization of both sets of lines (TP and SC) was the first step in this study. Briefly, GBS-derived SNP catalogs for the two sets were produced from an average of ~1800K reads per line for the TP (44K SNPs) and ~850K/line for the SCs (19K SNPs). Overall, for the TP, the average proportion of missing data was 0.43 (before imputation) and the mean minor allele frequency was 0.25. For the SCs, the average proportion of missing data was 0.35 and the mean minor allele frequency was 0.32.
Training and Assessment of the Genomic Selection ModelWe set out to train a GS model and to test its accuracy first via cross-validation and then on a set of segregating lines developed in the UL breeding program. Phenotypic data for five traits (DON, HTM, MAT, TKW and GYD) over numerous environments (14 to 41 environments per trait) were collected for the 245 lines of our TP. Descriptive statistics are summarized for each environment and trait in Supplementary Data 2. We obtained moderate to high broad-sense heritability He2 as well as significant differences among lines (P-value < 0.05), as shown in Supplementary Data 3. The BLUE values exhibited a very good level of variation and a normal distribution for the five traits (Supplementary Data 4 and 5). As expected, some of the traits presented a strong phenotypic correlation. The highest correlations were obtained between HTM and MAT (0.70), TKW and GYD (0.46) as well as between DON and GYD (0.38) as the highest yielding lines accumulated more DON (Supplementary Data 6). These extensive phenotypic data were used to train the GS model with a GBLUPe statistical model. As a first assessment of the accuracy of the GS model, we performed a 60:40 cross-validation. On average, the accuracy ranged between 0.44 (for MAT) and 0.70 (for TKW) as displayed in Figure 1. Accuracies of GS were highly consistent with the nature of each trait. Known complex traits such as DON, GYD, HTM and MAT displayed the lowest values in comparison with a simpler trait such as TKW. In general, the model provided satisfactory accuracies.
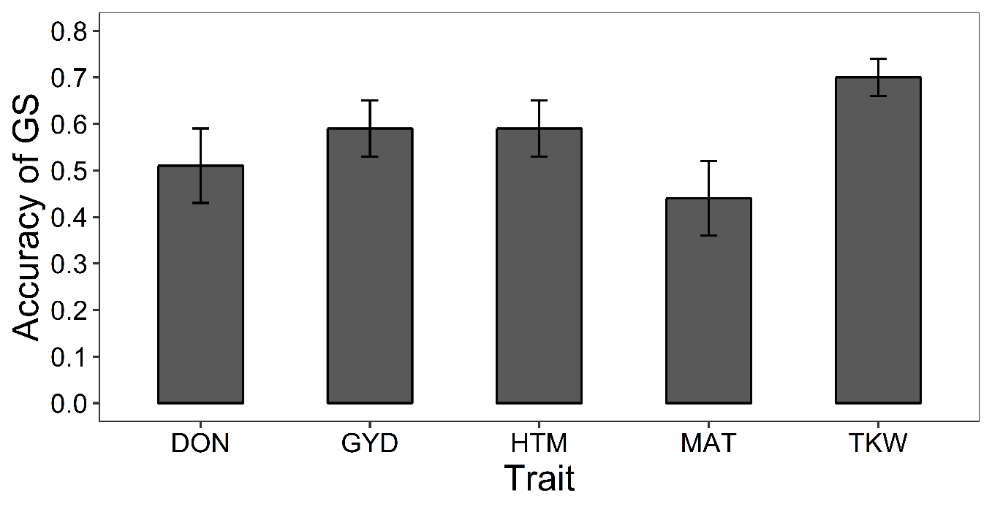 Figure 1. Prediction accuracies assessed through cross-validation (60:40). GBLUPe was used to predict the phenotype of barley lines for five traits [deoxynivalenol content (DON), heading time (HTM), days to maturity (MAT), thousand kernel weight (TKW) and grain yield (GYD)]. Accuracy was measured as Pearson’s correlation between predicted and observed performance in 100 validation subsets randomly chosen from the training population. Error bars represent the standard deviation of the mean.
Figure 1. Prediction accuracies assessed through cross-validation (60:40). GBLUPe was used to predict the phenotype of barley lines for five traits [deoxynivalenol content (DON), heading time (HTM), days to maturity (MAT), thousand kernel weight (TKW) and grain yield (GYD)]. Accuracy was measured as Pearson’s correlation between predicted and observed performance in 100 validation subsets randomly chosen from the training population. Error bars represent the standard deviation of the mean.
As a further assessment of the accuracy of the genomic selection model, we predicted trait values for 350 SC lines (based on their known genotype and using our trained model), selected the top 10% and characterized this set of 35 lines in the field. For these lines, phenotypic data (DON, GYD, HTM, MAT, TKW) resulted from trials conducted in two to four environments. For each environment and trait, descriptive statistics are displayed in Supplementary Data 7. For all traits and environments, we obtained moderate to high broad-sense heritability He2 and differences among lines were significant (P-value < 0.05) as shown in Supplementary Data 8. The descriptive statistics of BLUE values (displayed in Supplementary Data 9) showed a good level of variation among lines and environment. As expected, DON was the most variable trait among environments. Accuracy was measured both using Pearson’s correlation between predicted and observed (BLUE) trait values as well as between the ranking of the lines (Spearman’s correlation). The correlation between trait values was 0.47 for DON, 0.42 for GYD and 0.72 for TKW (Figure 2). However, for HTM and MAT, mean accuracies were much lower (<0.10). As for the correlation between ranking of the lines, these were 0.49 for DON, 0.45 for GYD, 0.72 for TKW and <0.10 for HTM and MAT (data for correlations by environment are provided in Supplementary Data 10). Overall, with the exception of HTM and MAT, the degree of agreement between predicted and observed trait values suggested that the GS model was providing an adequate degree of accuracy for the most important traits. Genotypic and phenotypic data generated from the study are available in Supplementary Data 11 and 12, respectively.
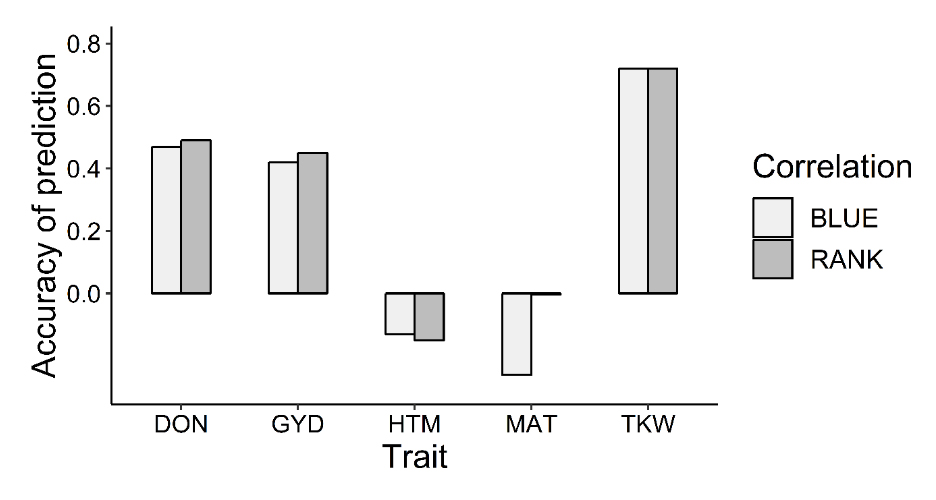 Figure 2. Prediction accuracies assessed through a validation process. The GBLUPe model was used to predict the phenotype of SC lines for five traits [deoxynivalenol content (DON), heading time (HTM), days to maturity (MAT), thousand kernel weight (TKW) and grain yield (GYD)]. Accuracy was measured as the correlation between predicted and observed performance and rank in the selected lines (top 10%).
Figure 2. Prediction accuracies assessed through a validation process. The GBLUPe model was used to predict the phenotype of SC lines for five traits [deoxynivalenol content (DON), heading time (HTM), days to maturity (MAT), thousand kernel weight (TKW) and grain yield (GYD)]. Accuracy was measured as the correlation between predicted and observed performance and rank in the selected lines (top 10%).
With the goal of producing simulated sets of progeny from all potential pairwise crosses between lines comprising the TP, it was necessary to provide marker data as well as genetic map positions for these markers. Of the 44K SNPs captured in the TP, 14K SNPs were successfully mapped onto the POPSEQ genetic map and had coherent physical and genetic positions. The resulting set of mapped loci was mostly clustered in the distal regions on the physical map but offered a fairly uniform distribution on the genetic map, with few gaps >10 cM (1 to 2 per chromosome; Supplementary Data 13). Using all 245 lines of the TP, a total of 30,000 possible pairwise crosses were simulated using PopVar. In each case, a set of 500 homozygous progeny lines was generated and, based on the genotype of each line, a trait value (GEBV) was predicted using the GS model previously built. Finally, we computed the mean (μ), the genetic variance (VG) and the mean value for the superior progeny (μsp; top 10%) for each trait and each simulated population.
As illustrated in Figure 3, for GYD, the crosses predicted to offer the highest (e.g., >5000 kg/ha) and the lowest (<4000 kg/ha) mean yield were also predicted to offer a limited variance. Conversely, only crosses predicted to have an intermediate mean yield offered a greater variance. In addition, as can be seen in the density plots above and to the right of the graph, the distribution of predicted variances was much narrower than the distribution of predicted means, the latter being much more uniformly distributed across the entire range of predicted values.
A similar pattern was observed for DON. Indeed, the high- (>50 ppm) and the low-accumulating (<20 ppm) crosses corresponded to the ones displaying a limited predicted variance, while a larger variance was obtained among crosses predicted to offer an intermediate mean DON concentration (around 40 ppm). Again, the distribution of predicted means was larger compared to the distribution of predicted variances as displayed in the density plots. Whether for GYD or DON, the pattern of μ and VG was similar as the majority of crosses were predicted to generate populations with variable μ but limited VG and few with moderate μ and large VG.
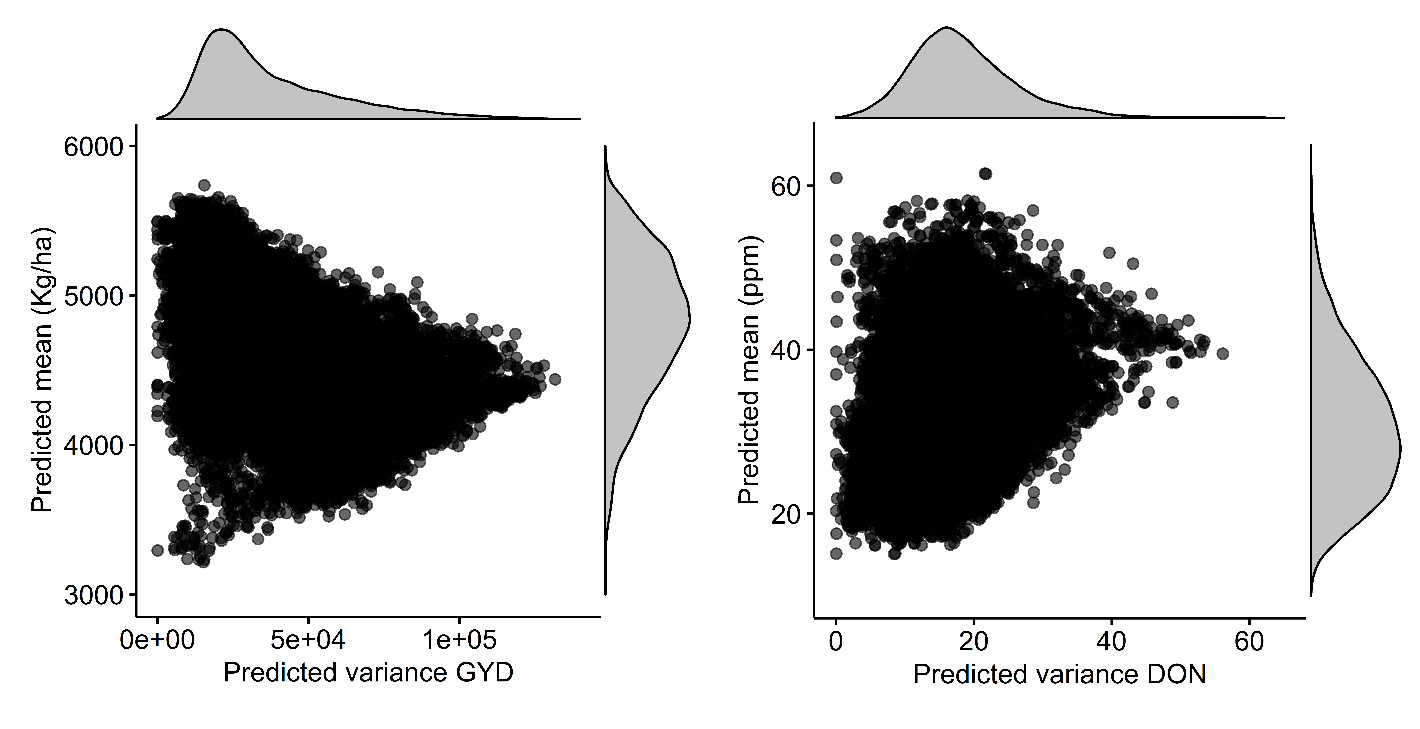 Figure 3. Pattern of relationships between predicted progeny mean and variance for all 30,000 pairwise crosses between the 245 lines in the TP. Each dot shows the predicted mean and variance for the genomic-estimated breeding values (GEBVs) of the progeny (RIL) from one cross. Results are shown for grain yield, GYD (left) and deoxynivalenol content, DON (right).
Figure 3. Pattern of relationships between predicted progeny mean and variance for all 30,000 pairwise crosses between the 245 lines in the TP. Each dot shows the predicted mean and variance for the genomic-estimated breeding values (GEBVs) of the progeny (RIL) from one cross. Results are shown for grain yield, GYD (left) and deoxynivalenol content, DON (right).
To assess the accuracy of the predicted value of a cross, we hypothesized that superior crosses would be expected to produce progeny that persist longer in the breeding program, i.e., advance to later stages of testing. To test this, we examined the persistence of progeny from 210 crosses that had already been made and evaluated within the context of two ongoing breeding programs (UL and Céréla). Depending on the trait that was known to have been emphasized during selection, two different situations needed to be considered. In a first case, as would be expected in most breeding programs, emphasis was placed mostly on GYD. In a second case, crosses were performed more in a pre-breeding context where emphasis was placed first on DON.
As displayed in the first case (Figure 4; UL program), we can see clearly that persistent crosses (≥F9) clustered together very tightly and were among the top ones in term of μ (≥5000 kg/ha); unsurprisingly these crosses had low VG. As expected, the situation was different in terms of the predicted DON for these same crosses. Indeed, the predicted means and variances for these crosses were quite scattered, with the predicted mean DON for some crosses exceeding the overall predicted average across all possible crosses (30 ppm). Moreover, in a different breeding program (Céréla), we observed a similar pattern of persistence of highly performing crosses in GYD (Figure 5). Such a clustering (for GYD) and scattering (for DON) of predicted means is consistent with expectations when emphasis is placed mostly on GYD during selection. Also, as hypothesized in the beginning, crosses predicted to be superior produced progeny that persisted longer in the breeding program. Indirectly, this suggests that the predictions made regarding the performance of the simulated crosses are not too far from reality. Conversely, however, crosses with the highest predicted mean µ were not necessarily the most persistent, suggesting that either the predictions proved relatively inaccurate or that perceived weakness in some other trait(s) could have led to the lack of persistence in the breeding program.
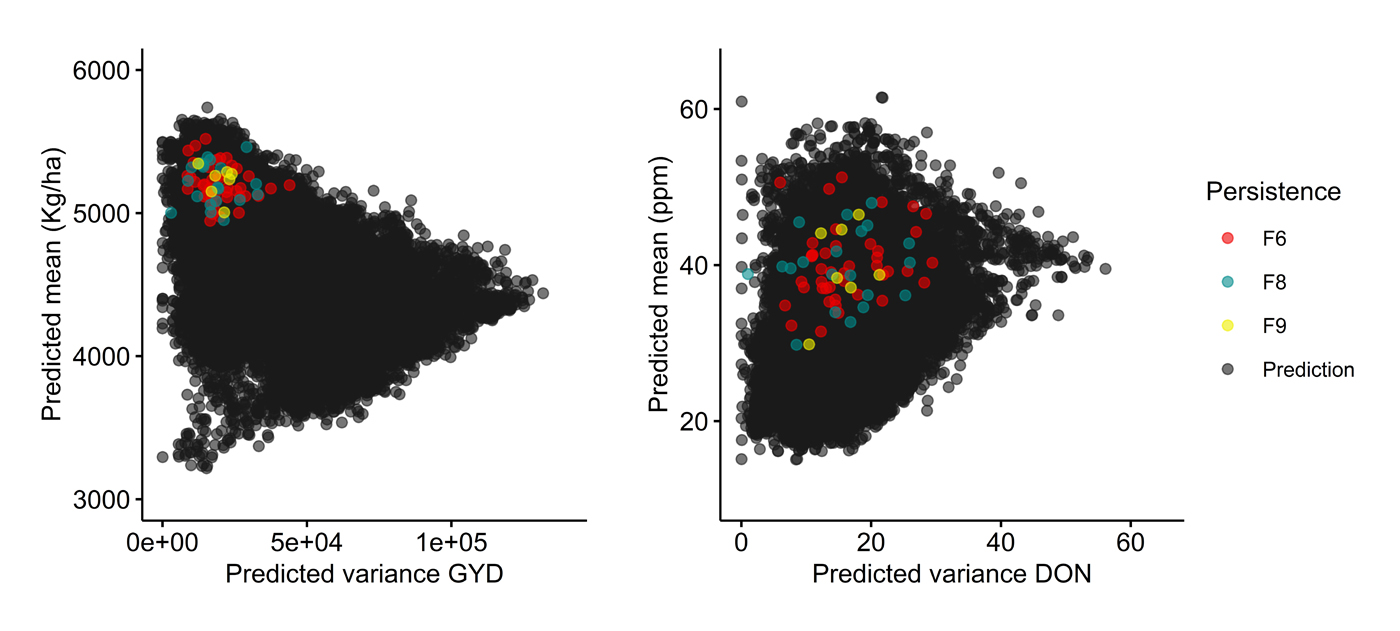 Figure 4. Persistence of crosses over the course of selection emphasizing grain yield (GYD) in the UL breeding program. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both GYD (left) and deoxynivalenol content, DON (right).
Figure 4. Persistence of crosses over the course of selection emphasizing grain yield (GYD) in the UL breeding program. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both GYD (left) and deoxynivalenol content, DON (right).
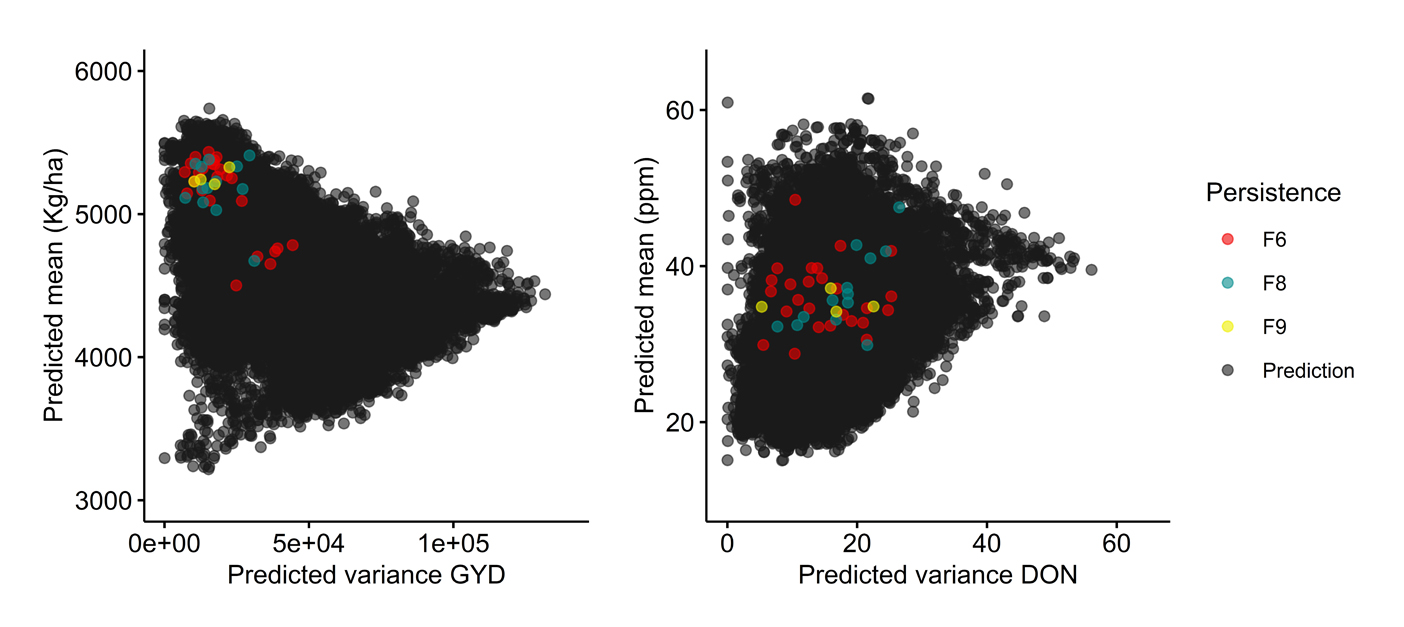 Figure 5. Persistence of crosses over the course of selection emphasizing grain yield (GYD) in the Céréla breeding program. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both GYD (left) and deoxynivalenol content, DON (right).
Figure 5. Persistence of crosses over the course of selection emphasizing grain yield (GYD) in the Céréla breeding program. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both GYD (left) and deoxynivalenol content, DON (right).
In a case where greater emphasis was placed on selecting parents likely to contribute to increased FHB resistance, and therefore reduced DON content (Figure 6), the pattern was quite different. The predicted mean GYD (as well as the predicted VG) for these crosses proved much more variable. Generally, crosses that persisted in the program were predicted to achieve a lower μ GYD (≤5000 kg/ha) compared to when this trait was emphasized. As for the predicted DON values among lines that persisted in the selection program, there was no evidence that this selection had been very effective, an observation which is not inconsistent with the inherent difficulties in obtaining reliable phenotypic data for DON on breeding materials. Again, the results obtained in terms of predicted means are not inconsistent with expectations in a pre-breeding context.
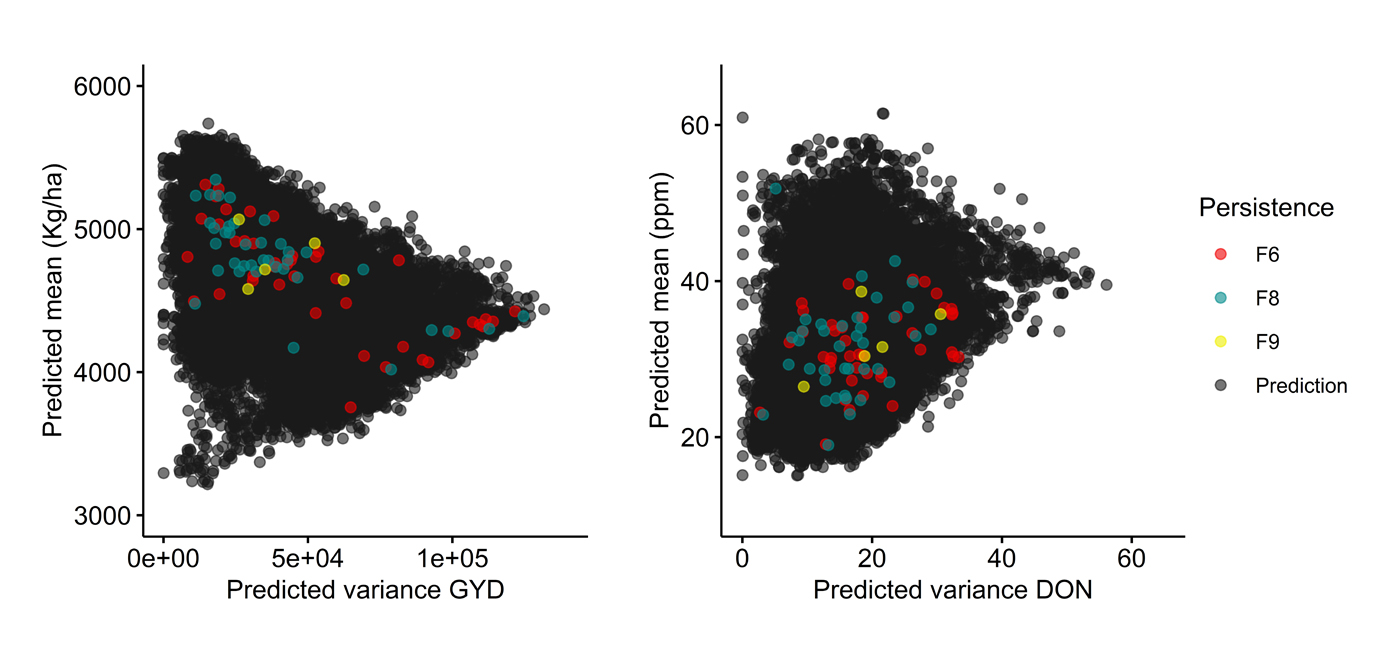 Figure 6. Persistence of crosses over the course of selection emphasizing fusarium head blight (FHB) resistance [low deoxynivalenol content (DON)]. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both grain yield, GYD (left) and DON (right).
Figure 6. Persistence of crosses over the course of selection emphasizing fusarium head blight (FHB) resistance [low deoxynivalenol content (DON)]. Grey circles (black upon overlap) indicate crosses whose performance was predicted but were never made, while red, blue and yellow circles represent crosses that were made and for which at least one progeny line was retained up to the F6, F8 or F9 generation and beyond, respectively. Crosses are plotted on the basis of their predicted mean (y axis) and variance (x axis) for both grain yield, GYD (left) and DON (right).
As described previously, one particular challenge of selecting for both GYD and DON is that these traits are highly and positively correlated, whereby the highest yielding lines typically (and undesirably) exhibit the highest DON values. We wanted to test if our simulated results captured such correlations in the hope that it might then be possible to identify crosses in which the correlation between these two traits were weakened. We first estimated the correlation between the predicted values for pairs of traits known to be highly correlated (rHTM-MAT, rGYD-TKW and rGYD-DON). As illustrated in Figure 7 the correlations obtained agreed with the expectations. Indeed, for HTM and MAT, the majority of crosses (96%) displayed a correlation ≥0.5 and the averaged correlation was 0.73. While for GYD and TKW, 40% of crosses had a correlation ≥0.5 with an average of 0.41. Finally, the unfavorable correlation between GYD and DON was also obvious as 50% of crosses exhibited correlations ≥0.5 and an averaged correlation of 0.47. These predicted correlations between traits were in very good agreement with the observed correlations between measured traits in the TP. The fact that these predicted progeny sets exhibited correlations between traits that were very close to the ones actually measured suggests that the proprieties of these simulated progeny are in agreement with what is expected for these traits.
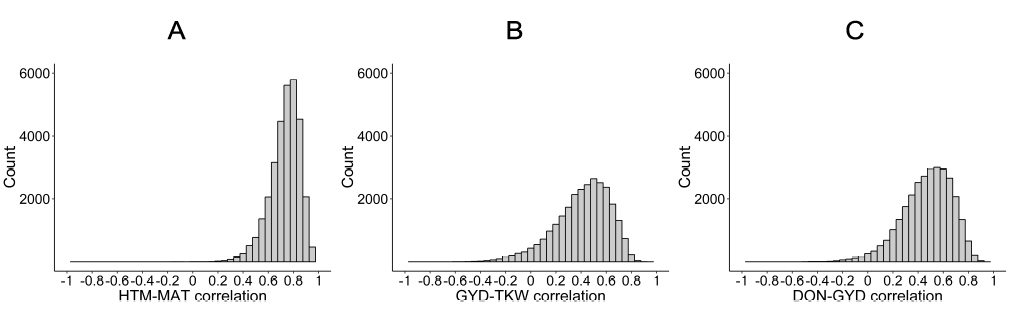 Figure 7. Correlations between GEBVs for three pairs of traits among the simulated progeny of all pairwise crosses between lines of the training set. Correlations are between: (A) heading time (HTM) and days to maturity (MAT), (B) grain yield (GYD) and thousand kernel weight (TKW), and (C) grain yield (GYD) and deoxynivalenol content (DON).
Figure 7. Correlations between GEBVs for three pairs of traits among the simulated progeny of all pairwise crosses between lines of the training set. Correlations are between: (A) heading time (HTM) and days to maturity (MAT), (B) grain yield (GYD) and thousand kernel weight (TKW), and (C) grain yield (GYD) and deoxynivalenol content (DON).
Having established from all that precedes that the predicted performances of simulated progeny sets reproduced the expected properties, we investigated whether it was possible to find crosses predicted to display a decreased (ideally, null or negative) correlation between DON and GYD. We found that 650 crosses were predicted to result in progeny sets within which this correlation was ≤0. We then inspected these crosses to identify ones predicted to offer an attractive level of GYD (eventually of DON). To establish such a performance threshold, we used the mean predicted trait values for checks commonly used in DON and GYD trials as a threshold beyond which we considered a cross as promising. We thus retained the subset of crosses for which the mean predicted GYD of the top 10% (μsp) ≥5000 kg/ha, while simultaneously exhibiting a low mean predicted DON (μsp ≤35 ppm). Ultimately, only 40 of the 650 crosses with low to negative correlation between GYD and DON met these criteria. Overall, of the 30,000 possible crosses that could potentially be made between TP lines, a mere 2.2% were predicted to show a low correlation between GYD and DONand a tiny fraction (0.13%) were predicted to produce progeny in which the top lines could combine high GYD with improved DON.
In this study, we tried to assess the reliability of a predictive model in an applied breeding context. A genomic selection model was used to examine the realm of possibilities among a large set of potential crosses. One of the focal points of this examination was to identify promising crosses in which the undesirable correlation between the most important traits in barley breeding (grain yield and DON accumulation) was predicted to be weakened.
To first establish the accuracy of our GS model, we measured its performance both via cross-validation and on progeny lines progressing through a breeding program. On average, we found the cross-validation accuracies to be satisfactory, as they ranged between 0.44 for MAT and 0.70 for TKW. These were very similar to previously reported results of cross-validation. In work on a similar set of agronomic traits, Nielsen et al. [50] obtained accuracies ranging from 0.40 to 0.83. Similarly, Thorwarth et al. [51] found that the prediction accuracy differed substantially between traits and that yield and thousand-kernel weight and heading date were among those showing the highest accuracy (0.74 to 0.83) very similar to results obtained in the current study. Finally, for DON content, Lorenz et al. [52] reported an accuracy of 0.37 (without correction for heritability), somewhat lower but similar to the value obtained here (0.5).
As a further assessment of the practical utility and accuracy of these predictions, we predicted trait values for 350 breeding lines and the top 10% was selected and characterized in the field. The degree of agreement between predicted and observed trait values suggested that the GS model was providing an adequate degree of accuracy for most traits (0.42 to 0.72) with the exception of HTM and MAT (−0.26 and −0.13). One of the possible challenges with the latter two traits is that the phenotypic variation in the training population is relatively narrow and possibly measured insufficiently precisely (every one or two days). Additionally, scoring HTM and MAT depends on breeder expertise and different breeders might have different scoring criteria. For the other traits, a similar magnitude of prediction accuracies has been reported in different studies. For DON, depending on the composition of the TP, predictive ability ranged from 0.42 to 0.49 in Lorenz and Smith [53]. Similar results were found by Sallam and Smith [10], with GS accuracies ranging from 0.19 to 0.43 for yield and from 0.25 to 0.75 for DON concentration (prior to correcting for heritability). Thorwarth et al. [51] evaluated the accuracy of prediction within families generated by intercrossing parents from old and modern cultivars. Similar to our results, they found that TKW showed the highest (0.71) prediction accuracy, while GYD exhibited the lowest value (0.31). Finally, across three cycles of genomic selection, Tiede and Smith [54] recorded correlations ranging from 0.07 to 0.36 for GYD, and from 0.17 to 0.37 for DON. Overall, the results of these two different assessments of the accuracy of our trait predictions suggested that they were consistent with what other researchers have reported and therefore broadly suitable for making predictions on potential crosses involving parental lines that were part of our training population.
Are Predictions of the Potential Performance of Crosses Accurate Enough?In view of estimating the potential performance of crosses among lines in the TP, a total of 30,000 possible pairwise crosses were simulated. Trait values (GEBVs) were predicted and the mean (μ), the genetic variance (VG) and the mean value for the superior progeny (μsp; top 10%) for each trait and each simulated population were computed. Whether for GYD or DON, and as found in many previous studies [2,4,17,20], we observed what these last authors [2] termed a “triangular pattern” where potential crosses with extreme μ (high or low) were accompanied by low VG, but crosses with an intermediate μ were associated with higher VG. Neyhart and Smith [2] explained this pattern by the fact that lines with similarly extreme phenotypes will probably share alleles at the majority of quantitative trait loci (QTLs) underlying a trait, thereby reducing the variation in the progeny of such crosses. This pattern was also predicted earlier based strictly on quantitative genetic principles by Zhong and Jannink [55]. Additionally, whether for DON or GYD, the distribution of predicted variances was much narrower than the distribution of predicted means, which were much more uniformly distributed across the entire range of predicted values. As no prior work has explored results from this point of view, we cannot compare our results.
We then performed what we refer to as “retrospective validation”, an approach where we examine the fate of crosses that were made within a breeding program. In this approach, we hypothesize that superior crosses will produce progeny that persist longer (e.g., ≥F9) in the breeding program. Depending on the trait emphasized during selection, two different situations were investigated. In a first case, a conventional cultivar development process was examined where the primary emphasis of selection was placed on GYD. In both the UL and Céréla breeding programs, persistent crosses shared a high predicted μ and low VG. Conversely, the predicted μ and VG for DON were quite scattered, typically displaying high μ in persistent crosses. In a second case, more closely resembling a pre-breeding process where primary emphasis was placed on DON, the observed pattern was quite different. Predicted μ and VG for GYD proved much more variable. Generally, crosses that persisted in the program were predicted to achieve a lower μ GYD compared to when this trait was emphasized. For DON, predicted μ among persistent lines showed a trend to lower values compared to the first case. In general, depending on the trait emphasized during selection, the results obtained in terms of predicted means were consistent with expectations. For some crosses, despite being predicted to offer a superior trait value (for GYD for example), they were removed in early stages of selection. Although this may seem counterintuitive, it could stem from selection for some other trait not considered here. For example, a cross could be accurately predicted to present a very high yield potential, but never achieve it in practice due to lodging. In such as case, despite a high predicted mean yield among progeny, a cross could be eliminated fairly early on this basis.
Based on these results, it seems that in a conventional breeding context, breeders tend to choose high-yielding parents that are likely genetically close, and thereby generate progeny with low variance. In contrast, in a pre-breeding context, breeders tend to choose at least one parent assumed to offer some desired trait (e.g., resistance to FHB) but more genetically distant from the other (presumably better from an agronomic standpoint), thereby producing a large variance (in GYD and DON). It is not evident that this selection has been very effective as the gain in terms of reduction is DON levels is very low compared to the loss in terms of yield. This is not entirely surprising as selecting for resistance to FHB is tremendously challenging given the difficulties in obtaining an accurate measure of the phenotype in the context of a breeding program, especially in the early generations.
While the general features described above were in agreement with the expected properties of crosses that show persistence within a breeding program, these data do not formally constitute a direct validation of the accuracy of these predictions. To the best of our knowledge, no similar retrospective validation has been reported in the literature. Instead direct validation has been attempted but on a very limited scale. In fact, in barley, we are aware of only two such reports where genomic predictions were directly compared to the actual performance of crosses measured in the field. Tiede et al. [30] were the first to explore the accuracy of genetic variance prediction via direct validation. They recorded a good accuracy (correlation of 0.61) for FHB severity when using a method based on simulated populations (PopVar). Recently, Neyhart and Smith [2] assessed the accuracy of predic tions of the mean and genetic variance within a contemporary barley breeding program for three key traits. These authors found that progeny means could be predicted with a fairly good accuracy (correlations ranging between 0.46 and 0.69; mean = 0.54), but it proved much more challenging to accurately predict genetic variance, with correlations between predicted and observed variances averaging only 0.29 (ranging from 0.01 to 0.48). Similar conclusions were reached by Adeyemo and Bernardo [14] in maize. In wheat, Lado et al. [17] found that, when predicting superior crosses, the importance of modeling the variance was trait specific [19]. These results suggest that although genomic prediction methods can accurately predict overall progeny means, the accurate prediction of variance remains challenging and will require more work. As a consequence, at this time, the selection of crosses that present similarly high means but differ in their predicted variance (and thus the predicted mean of the superior progeny) must be viewed as an uncertain outcome.
Correlations between DON and GYDOne particular challenge of selecting simultaneously for GYD and DON is that these traits are unfavorably correlated. If it were possible to identify crosses in which this correlation is reduced or abolished, this would greatly facilitate making genetic gains on both fronts. We first examined the correlations between predicted values for pairs of traits known to be strongly correlated. Among simulated progeny, for all three pairs of traits, strong correlations (0.41–0.73) were observed and these were very similar to the degree of correlation known to exist between these traits among lines of the training population (0.38–0.70). Few studies have investigated the magnitude of correlation among simulated progeny for these pairs of traits. Mohammadi et al. [20] focused on DON concentration and yield and reported an average correlation between GEBVs of simulated RILs of 0.31, comparable to what was obtained in the current study (0.41). More generally, this undesirable correlation has been observed within the University of Minnesota barley breeding program [20] and these authors have argued that this unfavorable correlation could be caused by linkage or pleiotropy.
We then investigated whether it was possible to find crosses predicted to display a weakened correlation between DON and GYD. We found that only 650 (2.2%) crosses were predicted to generate progeny with null or negative correlation between these two traits. Surprisingly, this is roughly four-fold less than 8.3% (36 of 435) reported by Mohammadi et al. [20]. In the latter case, these correlations were computed from a small subset (30 randomly-selected parental lines) rather than the entire set of potential parents as was done here. Alternatively, the observed difference in the proportion of crosses with null/negative correlation might be due to differences in the underlying genetic architecture controlling these traits in the two sets of germplasm.
We further inspected these crosses to identify ones predicted to offer an attractive level of GYD. When focusing only on crosses predicted to produce superior progeny exceeding the performance of selected high-yielding checks in variety registration trials, only 40 crosses (0.13%) were also predicted to exhibit a null/negative correlation between GYD and DON. As no similar analysis was conducted in the work of Mohammadi et al. [20], we cannot compare our results. Nonetheless, the extreme rarity of crosses in which an attractive yield is combined with a broken or even favorable correlation between GYD and DON is consistent with the difficulties experienced by breeders in developing improved lines with higher GYD and lower DON. If such predictive approach were to provide breeders with a tool to identify exceptional crosses in which gains for both traits could be achieved, this would be a great step forward. However, we stress the fact that the promising crosses reported in this work should be validated in the field prior to any large-scale adoption of such an approach.
We assessed in this study the reliability of a predictive model in an applied breeding context. The degree of agreement between predicted and observed values for DON, GYD and TKW suggested that the GS model was providing an adequate degree of accuracy. Whether for GYD or DON, the pattern of µ and VG was similar as the majority of crosses were predicted to generate populations with variable µ but limited VG and fewer exhibiting moderate µ and large VG. To assess the reliability of the predicted value (µ and VG) of a cross, we used a retrospective approach whereby we followed the persistence of crosses through the course of the breeding process. Crosses predicted to be superior produced progeny that persisted longer in the breeding program. This suggests that the predictions made regarding the performance of the simulated crosses are not too far from reality. The predicted correlations between traits known to be correlated (e.g., DON-GYD) were concordant with observed and expected correlations suggesting that the properties of these simulated progeny are similar to what is expected for these traits. Overall, of the 30,000 possible crosses that could potentially be made among lines comprising the training population, only 2.2% were predicted to show a low correlation between GYD and DONand just 0.13% were predicted to produce progeny in which the top 10% lines could combine high GYD with improved DON.
Most breeders will admit that outside of specific situations (e.g., introgressing a particular gene), selecting the crosses made in a breeding program is not the most data-driven aspect. Introducing an element of genomic prediction at the cross-selection stage (genomic mating) is much more palatable to established breeding programs than at later stages (genomic selection), such as selecting the best progeny. Indeed, using genomic selection during the actual selection phase entails major changes in resource allocation (from performing field trials to generating and processing genomic data)[11]. In contrast, using genomic prediction methods to identify promising crosses can be introduced into a breeding program with much more limited impact on how it is run. Even in the absence (as of yet) of empirical proof that genomic prediction can outperform current practice, many breeders will be willing to at least explore the potential of such an approach by allowing a portion of their yearly crosses to be selected on this basis.
Supplementary Date 1-10,13 (PDF, 1.82 MB)
Raw data (genotypic and phenotypic) used in this study are available in “Supplementary Data 11” and “Supplementary Data 12”.
A. Abed and F. Belzile designed the study. A. Abed performed field and lab experiments, the bioinformatics and statistical analyses, and interpreted the results. A. Abed and F. Belzile wrote the manuscript.
The authors declare no conflict of interest.
This study was funded jointly by the Natural Sciences and Engineering Research Council of Canada and by Céréla Inc. through a Collaborative Research and Development grant. The funders had no role in study design, analysis or preparation of the manuscript.
We are grateful to Martin Lacroix and Suzanne Marchand (Université Laval) as well as to Annie Archambault and Samuel Ostiguy (Céréla) for their assistance with various aspects of this work.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
Abed A, Belzile F. Exploring the Realm of Possibilities: Trying to Predict Promising Crosses and Successful Offspring through Genomic Mating in Barley. Crop Breed Genet Genom. 2019;1:e190019. https://doi.org/10.20900/cbgg20190019

Copyright © 2020 Hapres Co., Ltd. Privacy Policy | Terms and Conditions